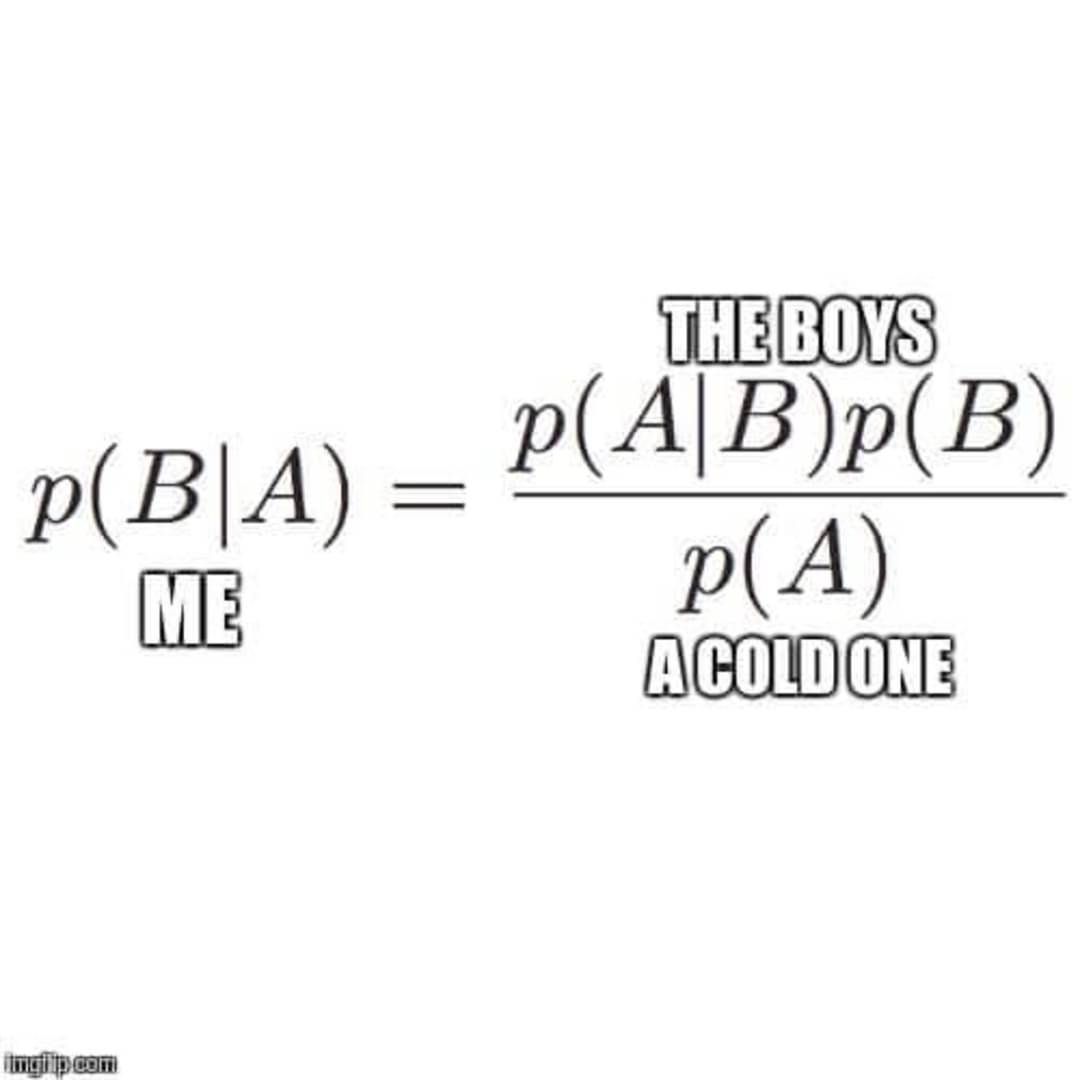Science Memes

10905 readers

1498 users here now

Welcome to c/science_memes @ Mander.xyz!

A place for majestic STEMLORD peacocking, as well as memes about the realities of working in a lab.

Rules

Don't throw mud. Behave like an intellectual and remember the human.
Keep it rooted (on topic).
No spam.
Infographics welcome, get schooled.

This is a science community. We use the Dawkins definition of meme.

Research Committee

[email protected]

Other Mander Communities

Science and Research

Biology and Life Sciences

Physical Sciences

Humanities and Social Sciences

Practical and Applied Sciences

Memes

Miscellaneous

founded 2 years ago

MODERATORS

[email protected]

Can't wait for the weekend. (mander.xyz)

submitted 5 months ago by [email protected] to c/[email protected]

5 comments fedilink hide all child comments

top 5 comments

sorted by: hot top controversial new old

[–] [email protected] 7 points 5 months ago

This isn't a meme I can enjoy frequently....

[–] [email protected] 5 points 5 months ago (1 children)

Ok, this is Bayesian probably update. Is is said that posterior and the model crack the prior?

What am i missing?

[–] [email protected] 1 points 5 months ago

I know it's referencing this but don't know enough about Bayesian probability

https://knowyourmeme.com/memes/cracking-open-a-cold-one-with-the-boys

[–] [email protected] 3 points 5 months ago (1 children)

Can someone explain for the non-statisticians?

[–] [email protected] 2 points 5 months ago

P(A|B) means the conditional probability of event A happening if B has happened. It is defined as P(A∩B)/P(B).

The equation show is the Bayes' Rule. It shows the relationship between P(A|B) and P(B|A). This is useful in Bayesian statistics (of course why would it not be) as you change your probability distribution based on the data observed, and almost every time it's easier to find the value by swapping the events.